

|
 |
||
|
When the proof engine is invoked to execute correctness checks, the grammar of any selected operation is scanned and a set of logic statements is generated that can be inspected with reportProofStatements or showProofStatements. These proof statements are described in the following subsections.
Every expression is scanned for the presence of division (divT[x,y] in the grammar) and for each case found the following is generated:
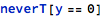
Every array access (partT[a,idx] in the grammar) is looked up for the array bounds in the array type definition (taking into account the starting index, which is configurable) and the statement is generated:
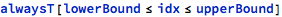
Package-level data objects and input (in and inOut) parameters are considered to be already initialized and as such compliant to their respective type invariants. These type invariants, when expressed in terms of respective objects, are considered as knowns.
Local variables have associated symbols initializedT[v], where v is the local variable name - this symbol is a Boolean variable that tells whether v was initialized; each local variable starts with its initializedT[v] counterpart set to False; the value becomes True when the variable is assigned to.
For each read access to the local variable v the following is generated:

At the end of the operation, each local variable is additionally checked for being initialized (if it is not initialized at the end of the operation, it means that it was never used at all):
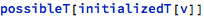
It is assumed that individual operators within expressions are executed from left to right. That is, for expression of the form:
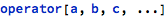
it is assumed that first a and b are acted upon, then the result is combined with c, and so on - this stepwise process creates N-1 subexpressions for each involved operator.
Each step in such computation is computed within the base type of its arguments - in the case of types derived from integer, the base type is integer. Every such subexpression is tested for the base type invariant, with type name replaced with the subexpression accumulated so far:

Such a series of checks allows to verify whether the stepwise execution always fits within the base type range.
Each complete expression is tested for the invariant of the target type, with type name replaced with the whole expression:

This check is generated in addition to subexpression checks and in some simple cases can appear redundant, for example in the following expression that involves integer variables:
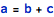
the check for subexpression b+c being within the base type (integer) is the same as the check for complete expression being within the target type (again integer). Such a pair of checks is no longer redundant if the target type (the type of variable a) is more constrained than the types of input variables.
Conditional control statements have conditions that are taken as knowns from the beginning of the respective branch. In the case of If statement, the “else” branch, if present, has the negated condition as its known.
Each conditional statement (If, While, Switch) has its main branch or each listed label tested for reachability, which is treated as an existence of some combination of values that makes the given condition True:
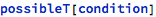
As a complement to this check, the reachability of the alternative branch is tested as well:

The reason for both of these checks is that if any of them would not be satisfied, this indicates a dead code in one of the branches (or the condition itself being always True, which is ineffective code).
The Switch statement deserves special treatment - if it contains the default branch, it is considered reachable when it is possible for the controlling variable to have a value that is different from all listed labels.
For each operation call its actual parameters of mode in and inOut are checked for being compatible with the invariants of the formal parameter types.
Within the operation body, its pre-conditions are checked for being reachable - that is, whether it is possible at all to satisfy them. Pre-conditions might be impossible to reach if they are self-conflicting or if they conflict with the invariants of involved types. For this, the following is checked together with the list of pre-conditions treated as knowns at the beginning of the operation body:
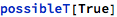
For each operation call its pre-conditions generate a single check that is a conjunction of pre-conditions for that operation, with parameter names replaced with the actual parameters:

At the end of operation body, its post-conditions are checked for being satisfied with the list of all accumulated knowns:

Post-conditions of called operations are handled similarly to call pre-conditions, except that their statements are not checks, but added to the list of knowns from the point of call onwards.
Explicit asserts are added to the list of generated checks verbatim:
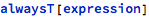
Explicit assumes are not added to the list of checks, but to the list of knowns. As such, they are not verification statements, but rather system boundary descriptions.
Previous: Grammar tags
See also Table of Contents.