

|
 |
||
|
Grammar tags are FMT’s symbols that are the building blocks for the internal model representation.
The reason such symbols were introduced is to replace the standard Wolfram symbols for various operations in order to prevent the kernel from executing some of the processing that is considered natural or expected in the world of mathematics, but that is not necessarily correct in the world of software engineering.
One example of such processing is the assumption that addition is commutative, which in Mathematica is implemented by means of Plus having the Orderless attribute. In other words, the following two operations:
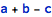
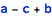
are considered equivalent by the Wolfram kernel.
In software engineering such assumption might be wrong, especially when range constraints are considered - for example, with machine integers of any limited bit length, if all three values are sufficiently large, the first operation above might overflow while the second one might be safe when executed from left to right. Other operations that might have unwanted standard effects are assignments (which can change the meaning of symbols used on the left-hand side) and control structures (which can lead to unintended evaluation when used in the model).
FMT also uses some syntax tricks in order to make the grammar more familiar to software engineers - for example, the structure field access, like in “point.x”, is implemented in terms of the Dot operation, which in Mathematica has the standard meaning of vector product.
In order to avoid such unwanted effects within the model, FMT replaces all standard operations with internal symbols. Additional symbols are used to make further analytics and proof operations easier. All such internal symbols are called grammar tags and are defined in the “FMTSymbols`” package. Most of the time it is not necessary for FMT users to know or use these symbols, but some guidance might be useful when diagnosing grammar errors, when the grammar tree cannot be completely reduced and when the analysis of partially reduced trees can make it easier to locate the problem. Advanced modeling techniques can also benefit from the explicit use of grammar tags to avoid unwanted evaluation of synthesized constructs.
The following sections explain all FMT grammar tags, grouped by contexts in which they can appear.
Standard types boolean and integer are internally represented by booleanT and integerT tags, respectively.
Empty statements are the simplest of all grammar constructs, as they represent the lack of operation in the place where some statement is expected by other grammar rules. The examples are an operation that does nothing or an empty body of the conditional If, Switch or the While loop construct.
Within the model the empty statement can be inserted with the standard Null symbol (the absence of this symbol where it is expected is an error, so empty statements are always explicit, except after the last semicolon in the compound statement), which internally resolves to empty statementT[]:
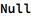

The statementT tags are also used as intermediate reductions of proper grammar constructs.
Compound statements are sequences of simple statements and can be used as complete operation bodies or as bodies of conditional or loop constructs. Within the compound statement subsequent statements are separated by semicolons:

Compound statement is represented by the compoundT tag, which wraps the whole sequence:
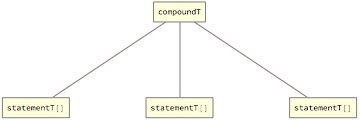
Non-empty statements within the operation’s body are numbered to make it easier to report errors and to locate them on control flow diagrams. Every non-empty statement is additionally wrapped by numberedT with consecutive index, assigned in a depth-first manner. Numbered statements are shown in later sections, although numberedT wrappers are abandoned in a very early stage of the grammar reduction process.
Literals are the simplest of non-empty grammar constructs, although they never form complete statements.
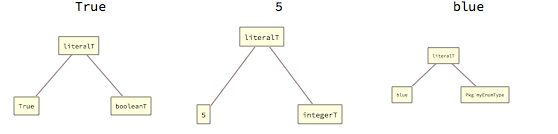
Literals can be Boolean constants (True or False), integer numbers or symbols introduced by definitions of enumeration types. The literalT tag wraps both value and type (if the type is defined by user, it will be always fully-qualified by its package name), for example:
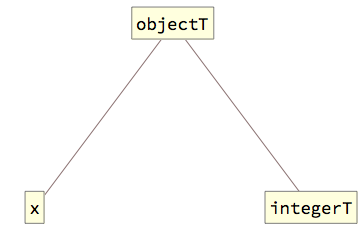
Whole objects, when they are accessed for reading, are wrapped by the objectT[] wrapper, which describes both the object and its fully-qualified type. For example, if x is an integer object, then accessing this object is represented as:
Similarly, when the object is accessed for writing on the left-hand side of the assignment operation, it is wrapped by the objectLhsT[] wrapper.
Accessing array elements is represented with the combination of objectT[] (or objectLhsT[], if assigned to) objectParentT[] and partT[] tags that refer to both the fully-qualified array object, the indexing expression and the extracted element type:
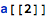
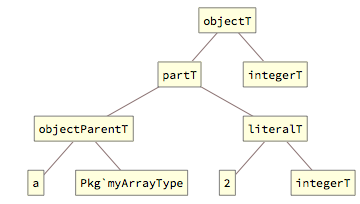
The objectParentT[] tag names the containing array object, together with its fully-qualified type - above, all three involved types (array type, indexing expression type and the array element type) are explicitly referenced.
The partT[] tag can be used to represent accesses to multi-dimensional arrays as well:
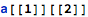
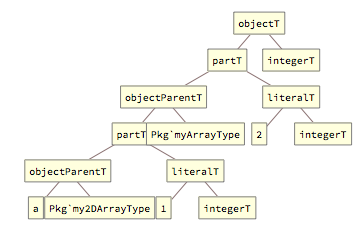
Above, the diagram layers of partT[] tags represent the steps of accessing the nested array element: first (at the bottom level), the 2D array is indexed to reference the nested 1D array, which is then accessed to obtain the final integer object.
Similar rules apply when accessing structure fields, where the dotT[] tag is used to bind both the parent object (the structure) and the named field. The internal representation is analogous to array accesses:
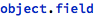
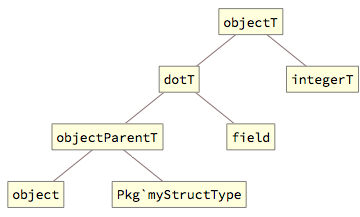
The dot[] wrapper can represent chains of accesses to nested structures (the pattern is similar to partT[] for multi-dimensional arrays, described above):

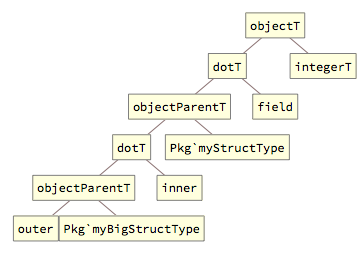
This scheme is both flexible (arrays of structures as well as array fields can be mixed in a single chain) and consistent, as the second element of objectT[] is always the ultimate accessed object type.
A complete assignment operation is internally represented with an assignmentT[] tag referring to both target object and the source value:
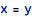
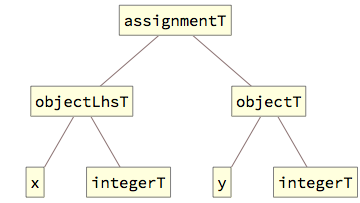
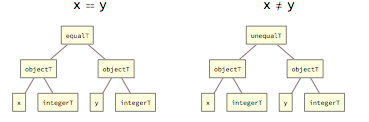
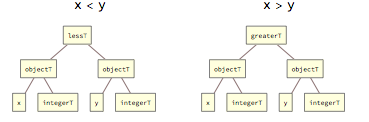
Relational operations allow to compare values of any standard type and always produce results of type booleanT. They are represented internally with tags equalT, unequalT, lessT, greaterT, lessEqualT and greaterEqualT:

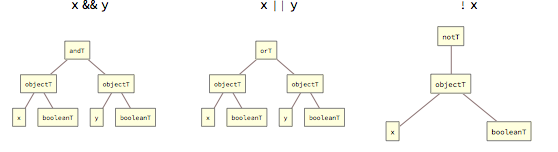
Logic operations act on and produce results of the booleanT type - they are internally represented by tags andT, orT and notT:
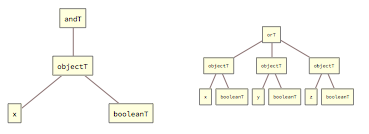
Tags andT and orT accept 1 or more arguments:
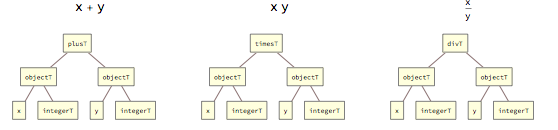
Arithmetic operations are represented by tags plusT, timesT and divT:
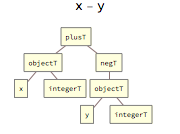
There is no separate tag for subtraction, which is instead represented by a combination of addition (plusT) and negation (unary negT):
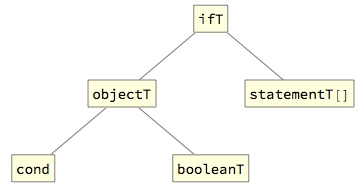
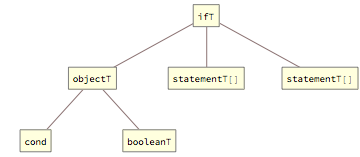
The standard If statement exists in two forms - with or without the “else” branch and is represented by the ifT tag, with two or three elements, where the optional third element contains the “else” branch:


The Switch statement, accepting only an enumeration object as its controlling value, is represented by the switchT tag. Case labels can be either single enumeration literals, alternatives (wrapped by the alternativesT tag), or optionally the Blank symbol (replaced by defaultT[] tag) for the default branch:

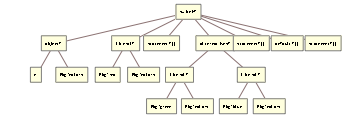
There is one basic form of looping: the While loop that reuses the standard Wolfram syntax. Other forms (like For) can be implemented in terms of preprocessor and as such do not exist at the grammar level.
The While loop is represented by the whileT tag:

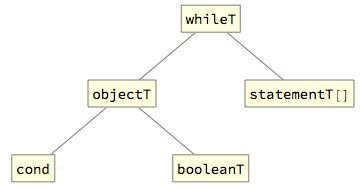
Operation calls are quite complex from the grammar perspective, because they can contain references to multiple parameters of different modes and types. In order to facilitate the detection of mismatches between expected (formal) parameters and the ones provided (actual) in the call, the operation call is translated into a structure of tags that carry complete information about both formals and actuals; the grammar engine then uses pattern matching tests to check whether parameters match and performs grammar reductions base on this matching.
All operation calls are represented by the callT tag, which wraps all information necessary to perform the parameter matching.
Calls to operations that have zero parameters look like in the following diagram:

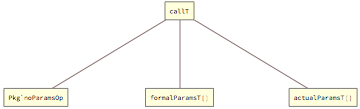
Above, the first element wrapped by the callT tag is the fully-qualified operation name; the second and third elements are nested lists of formal and actual parameters - in this case empty.
Calls to single-parameter operations (assuming the single parameter is of mode in and integer type) show how this structure is extended:

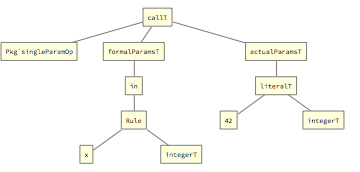
In this case formalParamsT and actualParamsT wrap one element and the grammar reduction engine can match them as compliant.
Calls to binary (that is, with two parameters) operations follow the same pattern:

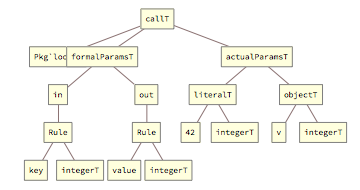
During the grammar reduction process, in the intermediate steps, the matching parameters are replaced with the matchingParamT tag; when all parameters are replaced by this tag, the whole callT structure is reduced to statementT[].
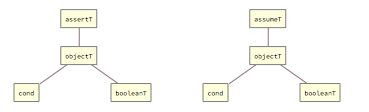
Assertions and assumptions are not imperative and executable statements, but logic conditions that take part in formal proofs. Assertions verify whether some condition is true, whereas assumptions state new facts that the engineer knows about, but that might not be automatically induced by the proof engine. These constructs are represented by tags assertT and assumeT, respectively.

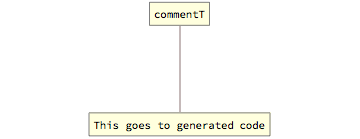
Injected comments are strings that instead of being immediately ignored by the Wolfram parser, are injected to the final generated source code and comments in the target programming language. These are mostly useful for injecting traceability links to higher-level artefacts, but can be used for any other purpose as well.
Injected comments are represented by the commentT tag, which wraps the actual comment string.

Some grammar tags are not used to represent code entities, but exist only temporarily to capture intermediate steps in the grammar reduction process. Still, it is possible for the user to see them occasionally, especially when analysing grammar errors, which are manifested by partially reduced grammar trees.
One such tag is the matchingParamT mentioned above, which expresses the fact that the actual parameter at the relevant position in the operation call matches the expected (formal) parameter - when all actual parameters become matchingParamT, the whole call is considered correct.
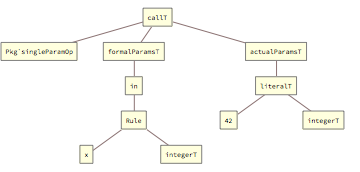
For example, for a single-param operation declared and called as follows:

the call is internally represented as:
and the next step in the grammar reduction process uses matchingParamT to indicate that an actual (provided) parameter was found to be matching its formal (declared) parameter:

Such a structure, where actualParamsT list contains only matchinParamT tags (or is empty), satisfies the grammar-reduction engine and the next step for the whole call is just statement[].
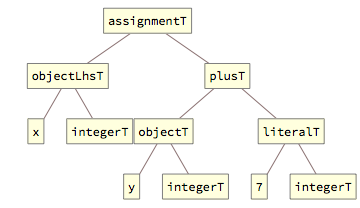
Other intermediate tags include exprT, which captures the type of some expression or subexpression during its reduction. The reason for this tag to get stuck in the reduction process is a type mismatch within the scope of the enclosing expression. The exprT tag wraps the type of the subexpression that it replaces.
For example, for the following expression:
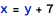
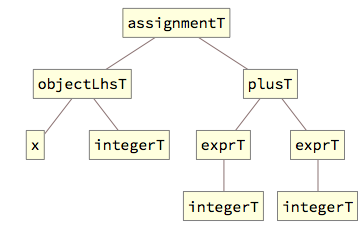
the tag exprT is used, in the next reduction step, to capture both the integer object and the literal (but still as separate arguments to plusT):
In such a structure, plusT can be recognized as a proper expression of type integerT itself, so exprT is again used to capture it:
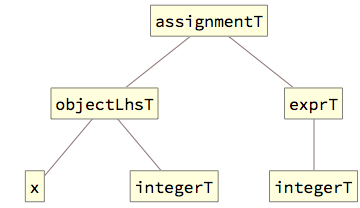
This is sufficient for the grammar engine to reduce the whole assignment to statement[].
Finally, lockedLiteralT captures the literal value that is used as Switch label, to prevent it from being automatically replaced with exprT of the literal’s type (which in this context is some enumeration type), which would hinder further checks like label coverage.
For example, in the following Switch statement:

the complete grammar tree looks like:
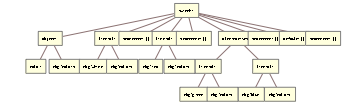
In subsequent steps, however, the literals, which would be replaced by exprT in any other context, are replaced with lockedLiteralT to prevent them from being seen as generic expressions:
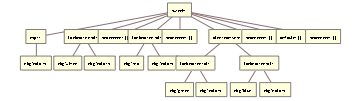
Such a construct is then analyzed for completeness and reduced to statementT[] if the check is positive.
Previous: Generating MISRA-compliant code, next: Proof statements
See also Table of Contents.