

|
 |
||
|
Apart from the most trivial examples, system modeling is a long-term activity that requires strong support for persistency as well as version control. Fortunately, all such issues can be solved at the level of Mathematica, without the need to provide any dedicated persistency features within the FMT toolkit.
Mathematica notebooks are natural containers for FMT models and in many cases the bare fact that notebooks are regular files will sufficiently solve all persistency needs. Interestingly, they also happen to be encoded as plain text files, so even though formatting and graphics need a large number of annotations and supporting information, the whole file can be stored and processed as text. This applies also to the possibility to use version control related utilities like diff.
Another option is the use of Wolfram scripts for modeling, instead of format-rich Mathematica notebooks. Scripts are much simpler to manage in that they do not support any formatting or embedded graphics, but their advantage is that they do not rely on any implicit information and the file content is exactly what engineers work with. This makes it even more straightforward to work with existing version-control tools, including reliable file merging.
But these are not the only options. Other possibilities can be found by exploiting the fact that FMT models are regular Wolfram objects that can be manipulated, copied, exported and imported like any other object.
For example, the following model:

can be cloned:
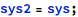
The two models, sys and sys2, are now distinct and changes in one of them (like new declarations or definitions) have no impact on the other one.
Models can be explicitly exported to files:

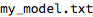
The file named in the Export function will contain the Wolfram expression that entirely defines the object. It is a text file that can be inspected and processed (and hacked) with regular text-processing tools.
Models that were saved this way can be read back by means of Import:

The sys3 model is now the same as sys:
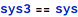

The Wolfram documentation chapter about Persistent Storage describes these and other possibilities, including both local and cloud storage.
Previous: Comments and traceability, next: Getting more from Mathematica
See also Table of Contents.