

|
 |
||
|
Operations are those model entities that encapsulate actual execution steps (statements) of the program and correspond to subprograms in regular imperative programming languages.
Operations are modeled within packages in two separate steps:
These concepts are familiar to engineers using imperative programming languages that promote the separation of specification and implementation - all target programming languages (Ada, C and C++) have this property. Still, this distinction is more pronounced with formal methods, which are not concerned with the actual execution anyway and can infer a lot of information from how the program entities are used, even without inspecting their internal definitions. In this context the operation’s declaration alone can be sufficient to analyze the correctness of the call site even if the definition (the operation’s body) is not yet written. Another case where the definition can be postponed is when the engineer intends to implement it outside of the FMT scope, perhaps to benefit from language features and coding patterns that are not directly supported by FMT.
Operations can be declared in a way that is similar to data types and package-level data objects, but the declaration syntax is much more elaborate to support all necessary information.
In the simplest case the operation has no parameters and no pre- and post-conditions:

Above, simpleOperation and otherSimpleOperation are operation names and empty brackets indicate that these operations have no formal parameters. Such an operation can interact with the rest of the model by calling other operations or by accessing package-level data (from the same or other packages).
Similarly to data types and data objects, it is possible to declare many operations in a single invocation of declareOperations and operations can be re-declared, which is signalled with a warning message. As with other entities, it is not possible to remove operations that were already declared and if such a need arises, the whole model needs to be reconstructed.
It is possible to declare formal parameters for operations. Parameters are named objects that exist only when the operation is executed and that are used to exchange values with the calling context - this value exchange can have three different modes:
These concepts are familiar to Ada programmers and they are also mapped directly to the same language features in Ada. For C and C++ the code generator uses conventional means like pointers and references in order to implement out and inOut modes.
The parameters can be of any type that is already known in the model, including types defined in other package (in which case they have to be fully-qualified by their containing package name), for example:
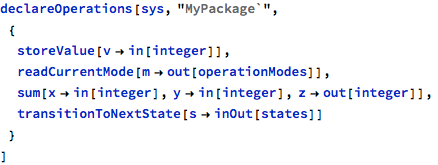
Above, the storeValue operation has only one parameter of type integer, which is passed by the caller. It is not possible for this operation to pass any value back to the caller (except perhaps via package-level data). Similarly, readCurrentMode transfers some value to the caller via its parameter, ignoring any previous value that the caller might have before the call in the variable that is used as the actual parameter.
The sum operation shows that the out parameter mode is the simple way to transfer values to the caller. In fact, it is the only way (again, not counting a messy use of package-level data for this purpose), as there is no concept of return value. In other words, operations are not functions in the sense that would allow them to be used as terms in expressions. Conceptually, operations have direct analogy in Ada’s procedures. This might be considered as a limitation by those programmers who are used to liberal use of value-returning functions, but is a result of careful consideration for the subsequent presentation of generated checks and proofs. The lack of functions in the modeling language promotes the explicit naming of all intermediate computation values, which increases readability of verification statements (especially when complex post-conditions are defined for the operation), error reports and makes it easier to debug the code if necessary. In other words, if the sum of two values is needed somewhere, perhaps as part of a bigger computation, then it needs to be named - for example by means of a separately defined local variable. This also means that operation calls are always counted as separate statements - they have distinct numbers in grammar trees and are represented as separate nodes in call graphs.
Finally, transitionToNextState uses its only parameter to update (read and write) the value provided by caller.
Operations can have defined pre- and post-conditions, which together with invariants of all data types that are involved in the operation call (parameters and package-level data objects that are accessed by the operation) form a contract of the operation - in other words, what the operation expects when it is called and what it promises when it finishes. From all these, pre- and post-conditions are specified when the operation is declared:
From this description it can be said that pre- and post-conditions form a “proof boundary” around the operation body and in the current version of FMT this is indeed the case in the sense that bodies of called operations are not inspected when checking the caller. Only the contract that is defined by pre- and post-conditions (and by type constraints of involved objects) are taken into account, which means that callers can be analyzed before the called operation is implemented.
Pre- and post-conditions are defined when the operation is declared and they are added to the operation profile in an extended syntax, for example:

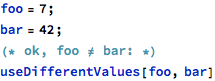
Above, there are two operations declared. The first is useDifferentValues with a pre-condition stating the expectation that the first argument (x) needs to be different than the second one (y) when this operation is called. The second operation, average, promises that the result, passed via the third out parameter, is a mean of the first two parameter values.
Pre- and post-conditions can be themselves lists, where multiple statements can be written as separate list elements. A list of separate statements is equivalent to a single logical conjunction of these statements.
Pre- and post-conditions represent statements that are not computed at run-time and in particular they do not need to be limited by run-time constraints of the imperative code. For example, in the average operation above, the fact that the sum of x and y might overflow before the value is divided by 2, is not a problem in the post-condition. The formula properly states the promise that binds together all parameters. In the operation body, however, the same formula might not be appropriate exactly for the reason of integer overflow in the intermediate subexpression, and the engineer implementing this operation needs to find some other way of achieving the same result - that is, the result that will satisfy the promise expressed in the post-condition.
Expectations and promises regarding any single argument can be equally expressed by means of pre- and post-conditions as well as type invariants. For example, the expectation that a single argument is greater than 0 can be expressed this way, with a pre-condition:

or this way, with a type sinvariant:

In both cases the caller needs to ensure that someOperation is called with an argument that is greater than 0.
The choice of the correct approach is a matter of engineering judgement, but the following simple guidelines can help to choose the best option:
In particular, pre-conditions are necessary to express conditions that are related to several parameters (or package-level data objects) at the same time, as it is not possible to write a single type invariant that will bind two distinct parameters (or data objects). The useDifferentValues and average operations shown earlier are possible examples where multiple values are bound by a single condition.
In some cases it might be necessary to refer to the initial value of some parameters in operation post-conditions. For example, in the increment operation that is supposed to update its parameter to the next higher value, it can be necessary to promise that the updated value is 1 greater than the initial (old) value. Similarly, in the swap operation that is supposed to exchange values of its two parameters, it might be necessary to express that the updated value of one parameter should be equal to the initial (old) value of the other parameter. There is a dedicated wrapper old that can be used to express such post-conditions:

The old wrapper is meaningless in pre-conditions, as all symbols have only their initial values anyway.
It is possible to provide both pre- and post-conditions for the same operation. For example, in the increment operation above, it might be necessary to express the limitation on the initial parameter value to avoid overflow when incrementing:

It is now the responsibility of the caller to ensure that increment is called with “safe” values only. Of course, a separate data type with invariants to capture the notion of “small and safe” value can be more appropriate in the given system, according to the guidelines above.
Special care should be taken with regard to comparisons in pre- and post-conditions. As in the examples above, equality is written with double-equal sign. Accidental use of a single qual sign (= instead of ==) will lead to unwanted symbol assignment, as pre- and post-conditions are not protected from evaluation. Further use of such accidentally assigned symbols might lead to error messages that are difficult to diagnose and explicit clearing of symbols with Clear (or restart of the kernel) can be necessary to re-establish the working environment.
Operation bodies provide the implementation part for already declared operations. It is worth restating that in some cases bodies do not have to be modeled at all (for example, when they are implemented outside of the model), so that it is possible to have operation declaration without body. It is not, however, possible to define the body of the operation that was not yet declared.
The operation body consists of the list of local variables and the sequence of imperative statements:

Local variables are declared in the list that is mandatory in the invocation of defineOperation. This list might be empty if the operation does not use any local variables, but the list itself cannot be omitted.
Variables are declared by rules that bind the variable name with its type, similarly to how operation parameters are declared, but without any mode, for example:

When declaring local variables, their type names are looked up with the usual convention - non-qualified names are looked up in the same package (so that colors and operationMode would have to be defined in the same package before the operation body is provided) while fully-qualified names can be picked from any package in the model.
It is not possible to provide the initial value in the list of variables. Each local variable needs to be assigned some valid value before it is read, but it is the proof engine that generates appropriate checks to verify that uninitialized variables are not used.
The sequence of operations that follow the (possibly empty) list of local variables can consist of empty statements, expressions, assignments, control structures and operation calls and additional annotations - all these building blocks are described in the following sections. Semicolons are used as separators between elements of this sequence, which means that the semicolon following the last statement is not necessary (in fact, if the trailing semicolon is written, Wolfram will implicitly add the Null value right after it, which is interpreted by FMT as additional and harmless empty statement).
Objects are accessed for both reading and writing by just naming them in expressions or in assignments or when using them as parameters in operation calls - the conventions are the same as in popular imperative programming languages. The context is used to distinguish between reading and writing, and in some cases the object can be used for both at the same time (like when using an object as an inOut parameter in the operation call).
Array elements are accessed using the standard Wolfram syntax, or rather any of the three standard ones, whichever is more convenient:
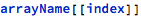


Double brackets are necessary in the first two variants and should not be confused with single brackets - they have different meanings in Wolfram.
The index should be an integer expression and the first index value is configurable - typically 0 or 1, depending on the engineer’s preferences.
Since there are no multi-dimensional arrays in the strict sense, only arrays of arrays, chains of brackets can be used to access elements deeper in the structure. Thus, for an array of integer arrays, the following is a possible way to access one of the elements:

Structure fields can be accessed using the “dot” convention known from other programming languages, for example:


The dot notation can be used to access nested fields if structures are used as fields in other structures, and the combination of array accesses with field accesses can be used as well:
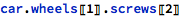
Special care has been taken to allow a seamless use of this syntax in operation bodies, but in rare occasions (especially in combination with syntax errors, which need to be analyzed) it might be useful to remember that even though the array access is a standard operation in Wolfram, the dot notation is built on top of the dot vector product, provided by the standard Dot function.
Empty statements are used, if ever, to fill the places required by grammar if there is no intended action in those places. The empty statement can even replace the whole operation body, but are mostly useful in conditional statements.
Examples of empty statements are (except the first, all others are supposed to be inside the body definition):
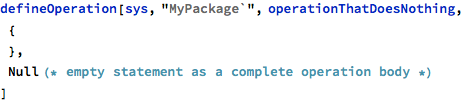



Perhaps the most useful place for an empty statement, however, is the empty Switch branch, which indicates that the given enumeration value was explicitly taken care of instead of being forgotten or implicitly covered by a generic default branch:

Expressions are not stand-alone statements, but are used to compute new values in other statements like assignments or conditional parts of control statements.
Expressions are checked for type correctness and those that do not conform in this regard are not matched by the grammar reduction engine - as a result, a type-incorrect expression will “get stuck” in the reduction process and will prevent the whole operation body from being validated.
There are intuitive analogies between expressions in FMT and in any of the target programming languages. On one hand, such analogies make the code generation process straightforward (and the generated code easier to verify) and on the other hand, the whole expression system in FMT can be described without unnecessary elaboration. Thus, example arithmetic expressions are:
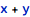
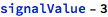

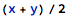
Relational operations are also expressions with Boolean results:

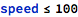
Example Boolean expressions can be:
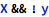

One of the most interesting aspects of working with Mathematica notebooks is that the front-end part of the system can be used to write and render expressions in several formats and the choice of particular format has no impact on how the kernel (back-end) part of the system operates. Thus, the above examples can be rewritten as:
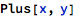


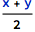
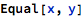
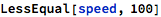


The last two examples of Boolean expressions can be also written in a “traditional form”, which bears strong mathematical esthetics:
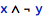

Choosing the right notation in a given context is a matter of engineering judgement, but some notes can help selecting the best option.
The “2D” way of writing division:
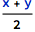
is visually pleasant and very readable, but has more complex encoding when notebooks are stored as files. Even though the underlying encoding is still based on pure text, the necessity to encode a more complex layout can have an impact on how easy it is to analyze output of external development tools like diff. Similarly, so-called full forms like Plus or Equal can look like unnecessary burden from the programmer point of view, but at the same time the unification of syntax that these forms provide can be very helpful in automatic model generators. In such contexts, pros and cons need to be evaluated and mature teams might want to take such issues under consideration in their coding standards.
Similar concerns apply also to the pre- and post-conditions (as well as type invariants), where expressions can be written using different formats.
Assignments are stand-alone statements (one of the consequences of this is that they are separately numbered on control flow diagrams) that allow to establish a new value for the whole object or a part of object. Examples of assignments are:
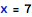
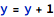

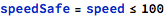
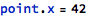

There are three basic control structures supported by FMT and all of them are familiar to engineers using any of the popular imperative programming languages.
The conditional If statement exists in two variants - without and with the optional “else” branch, which is consistent with the standard Wolfram syntax for this construct.
An example of the If statement without the “else” branch is:
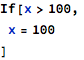
It is possible to have more statements in the conditional branch - the compound statement is a sequence of statements separated by semicolons:

The terminating semicolon after the second statement in the conditional branch above is not needed and if provided, it will be harmless and will implicitly inject an empty statement at the very end:

The “else” branch is optional, and can be provided after an additional colon:

Of course, if there is a need to write more statements in the “else” branch, they have to follow the same conventions regarding the use of semicolons as statement separators.
The While construct is used to implement loops:
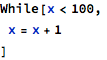
The rules for wring compound statements are the same as in the If statement, for example:

Finally, the family of control structures contains also the Switch statement, which is a multi-branch conditional statement driven by the enumeration value. As such, it is similar to the “switch” statement in C or to the “case” statement in Ada, but the difference is in the more limited set of allowed control expressions - the only allowed control expression is an object of some enumeration type. For example:

Above, color is an object (data object, parameter or a local variable) of some enumeration type. If this type is defined in the same package, it is possible to refer to enumeration values without qualification, otherwise full qualification by package name is necessary.
The Switch statement follows the standard Wolfram syntax for the Switch function - that is, odd number of elements is expected: the controlling value and then, repeated, the choice value followed by the branch. All used values have to be of the same enumeration type as used for the controlling variable.
Switch choices have to be single literal enumeration values (like white above) or alternatives, for example:

The same alternative expression can be written as:
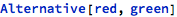
The meaning of alternative is to reuse the branch for several choice values - in the example above, the middle branch is executed when color is either red or green.
It is also possible to use the “default” choice, indicated by the Blank, shortly written as an underscore. Its meaning is to implicitly select all enumeration values that were not listed in other branches.
There are strict rules regarding the coverage of enumeration values: all values specified in the definition of the given enumeration type have to be covered (if they are not all covered explicitly, the default branch needs to be present) and the values cannot be used more than once in the same Switch statement.
Of course, if necessary, branches can be compound statements - sequences of statements separated by semicolons, with usual rules governing the use of such separators.
Operations, if already declared, can be called from other operations just as subprograms in any imperative programming language.
The operation call is a stand-alone statement and calls cannot be part of bigger expressions - after all, operations have no concept of a single return value that would allow them to be used this way.
Consistently with other visibility rules, operation names declared in the same package can be used without qualification, whereas operations from other packages need to be fully-qualified in calls. Any operation that was declared in the model can be called from any package and there is no concept of “private” visibility that would prohibit this.
If the called operation was declared with parameters, then actual parameters of appropriate types have to be provided in the call, otherwise empty brackets are required by the grammar.
Example calls to parameter-less operations can be (referring to declarations from the beginning of this chapter):
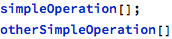
If an operation expects a parameter of mode in, it can be provided as a literal, an expression, or an object of appropriate type:
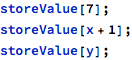
Parameters of mode out and inOut, however, can be filled with objects only:



In the operation call, the caller needs to ensure that operation pre-conditions are satisfied. If the pre-conditions refer to operation parameters, the pre-conditions are rewritten as checks with the use of actual parameters. Similarly, post-conditions, if they refer to parameters, are rewritten as new facts relating to objects that were used as actual parameters. Thus, reusing declarations from previous sections:


Operation calls gathered across the whole model form a call graph - even though it is not verified after implementing any single operation and is also not considered to be a grammar error, there is an overall check to ensure that the call graph does not contain cycles (in other words, that operations are not directly or indirectly recursive).
The FMT model can contain annotations that are not really executable statements, but instructions for a proof engine that express the expectations or knowledge of the engineer implementing the given operation.
An assertion is a check that some particular statement is satisfied. It reuses the standard Assert function with a single argument:

The logic statement written in the assertion is expected to be True under all possible circumstances in the given place - that is, under all possible executions. Such an expectation is typical, but not the only possible, as the gradation of expectations is more fine-grained and several wrappers are available to describe the design intent:



From these three possibilities, alwaysT and neverT are intuitively useful (and somewhat redundant, as logical negation is enough to transform between them), but possibleT deserves additional explanation: it is mainly useful to express the reachability of branches in control structures and the absence of dead code; the condition wrapped in possibleT is not guaranteed to be True, but it is guaranteed that for some combination of inputs, it is possible to achieve the given condition.
Assertions are fundamental building blocks of formal proofs and many of them are implicitly generated by the proof engine - for example, if there is a division in any expression, the assertion is generated to check that the denominator is never 0. Still, many assertions are also written manually to express expectations with regard to the program logic.
Assumptions differ from assertions in that they do not express expectations, but rather facts that are known to be true by means that are not visible in the model, but that the designer is convinced about by virtue of his system knowledge. For example:

The Assume function is not a standard Wolfram symbol, but is defined by FMT as a functional complement to Assert. Its name starts in uppercase for consistency with Assert - which intentionally breaks the recommended naming convention that reserves uppercase names for standard functions.
Previous: Data objects, next: Comments and traceability
See also Table of Contents.