

|
 |
||
|
Data types define the set of values that can be assigned to objects.
There are just two data types that are pre-defined in FMT:
Both standard types are pre-defined in a way that makes them visible in all user packages. No qualification is needed for these type names. Standard types can be used directly to define data objects or operation parameters and local variables, or as foundations to define new structural data types.
Numeric types can be defined in terms of the standard integer type and in addition to creating a new name for the type such definitions can refine the integer type with user-provided value constraints.
In the simplest form a new numeric type definition creates a new name for the standard integer type. Assuming that the model sys with package “MyPackage`” were already created, the following definition introduces a new numeric type that has the same properties as the standard integer type:

The function name and curly braces (indicating the list) suggest that it is possible to define multiple types in a single step:

It is possible to execute the defineDataTypes function multiple types for the same package, which will accumulate all new definitions, and it is also possible to replace the existing type definition with a new definition (not necessarily equivalent, as in this example). A warning message will inform the user that such a replacement is taking place:


There is no possibility to remove the named type definition - if this is actually needed, the whole system has to be recreated without the unwanted definitions.
Numeric types can be defined together with type invariants, which are constraints that all values of the given type should meet.
For example, a natural, positive and small integer types can be defined as:

As can be seen above, type invariants can be defined by means of any logic expression that refers to the newly defined type name as a placeholder for the value of that type. However, only constant values can be used in constraint expressions.
The meaning of type invariants is that whenever objects of the given type have new values assigned, the verification statement involving the given invariant will be generated and added to the set of statements that need to be proven at the given point - for example, in the case of positive type, the check will be generated to verify that the newly acquired value is greater than zero in addition to fitting in the integer range.
At the point of data type definition, no check is performed whether the invariant is self-consistent - this is verified together with all other checks generated at the point of use of the data object that was declared for the type in question.
Numeric types that share the same base type (currently integer is the only type that can be used as base) are compatible in the sense of assignments and they can be mixed within a single expression without type conversions. What makes such types different are their invariants.
Data types are visible in the same package without qualification, although full qualification can still be used for readability. When accessed from other packages, data object names need to be fully qualified. In other words, the type positive can be used by its short name within the “MyPackage`” package, but needs to be referred as MyPackage`positive when used in any other package. All defined types are visible in all packages within the same model, it is not possible to define hidden or “private” types for use within a single package only.
Enumeration types allow to define an explicit set of symbols that are used as values. Enumerations are limited in their usage patterns as they do not have any numeric interpretation and do not support any arithmetic-like operations. As such, enumerations are strongly typed and support only assignments and comparisons (which include their use in Switch control statements).
Enumeration types can be defined as in the following example:

Enumeration types cannot form hierarchies and cannot be constrained with additional invariants.
FMT supports fixed-length arrays, where the array element type can be any of the already defined data types.
An example integer array type of size 10 can be defined as follows:
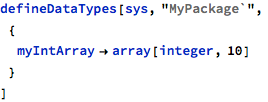
The array size should be a constant value.
Arrays are vectors in the sense that they are fixed-length sequences of values. This means that they are always indexed by integer values - no other index type (in particular enumeration) is supported.
One of the most contentious subject is the array starting index value, which itself is not visible at the point where the array type is defined, but does influence the element access operations, as well as verification conditions for index expressions. FMT does not attempt to solve this problem arbitrarily and instead allows the user to customize that value via configuration options. C and C++ programmers will very likely use 0 as a conventional first array index, while Ada programmers might prefer 1 as a starting point. These choices have no impact on the number of elements that the array contains - the example myIntArray type will have length 10 independently on the selected starting index, so valid indices will be 0..9 or 1..10. In any case, the generated source code will be correct for any of the supported programming languages and appropriate index offsets will be injected at all array access points, if necessary. The choice of starting index value has the scope of the whole model and affects all array types defined within the same model.
It is possible to define multi-dimensional arrays by means of nested array definitions:
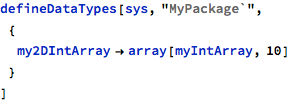
Above, my2DIntArray is an array of arrays, with 10x10 integer elements.
Structures allow to aggregate fields of possibly different types - any already defined type can be used to define a named field within the structure.
Example structures can be defined as follows:

It is possible to use other structure or array as a structure field type, as well as define an array of structures.
Previous: Packages, next: Data objects
See also Table of Contents.