

|
 |
||
|
This article belongs to the series documenting the reasoning behind and development of new features in the Formal Methods Toolkit.
The previous article presented how quantified statements about arrays can be introduced as assumptions (operation pre-conditions can be used for this, as well) and how the quantified statements propagate between array objects after they are modified. The next logical functionality in this area is the possibility to recover information (that is, “deduce” some facts) about objects from previous quantified statements. The design choice in FMT is to make this process explicit in the sense that the user should always indicate the quantified statement that is the source of deduction, although the indicated statement need not be syntactically equivalent to any of the statements already registered as “knowns”. The reason for this choice is two-fold: on one hand, explicit deduction makes the engineering intent clear and not surprising for the reviewer and on the other hand, such an explicitly expressed intent is a hint for the system that can make it easier to benefit from reasoning paths that might not be easily guessed by the more automatic approach.
In any case, the deduction process should take into account natural differences between the meaning of ForAll and Exists. For example, in the case of ForAll, if it is known that all values in the given region have some property (like: all array elements are 0), then it can be deduced that a given value within the region has that property (like: element at index 7 is 0 in that array). This simple deduction is not possible with Exists (like: there is 0 somewhere in the array), because it is never known whether the given element is the lucky one (like: it is not necessarily element at index 7 which is 0). It is justified, however, if the region happens to be a singleton with exactly one element (like: if the array has just one element, then that single element is the lucky one).
The differences between ForAll and Exists should be taken into account when matching expected statements with existing ones - for example, if there is a ForAll statement registered over some region, then ForAll over its sub-region is valid, too; in the case of Exists, a statement over a super-region is valid, if an Exists over the region is already known.
The deduction process uses the new Deduce operation, which similarly to Assert or Assume starts with capital letter, even though it is not a standard Wolfram symbol. The following example demonstrates the basic deduction from the ForAll statement:
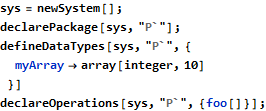

The proof statements show how the knowns are accumulated in each of the steps above:

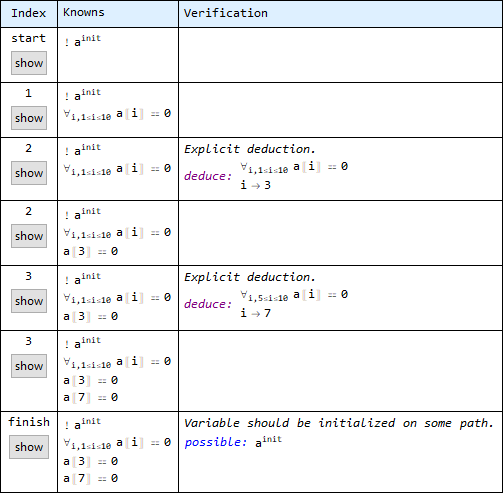
It can be seen that the quantified statement introduced at step 1. is later (at step 2.) used by means of exact matching to deduce that a[[3]]==0. The deduction over the sub-region at step 3. works as well.
The deduction operations are verified by checking that instantiation is within the given region and that the region is covered by known statements. The proof results show that everything is OK except for the uninitialized array, which is an expected failure in this example:

The system should be able to validate the user’s reasoning expressed in deductions. The following example demonstrates several wrong deductions:


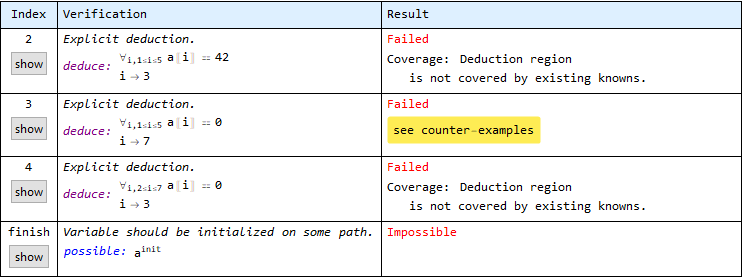
There are three wrong deductions in the code above and all of them are reported in the results table:
The above facilities allow not only to recover the knowledge about individual elements (for example, elements of some array) from quantified statements, but also to validate the reasoning behind them.
Further articles will demonstrate the induction and verification of quantified statements.