About Us Products Articles News Contact Support

Supporting Quantified Statements - Part 2

This article belongs to the series documenting the reasoning behind and development of new features in the Formal Methods Toolkit.

The previous article was a sketch of ideas for proper support of quantified statements in FMT. The basic building blocks, which are the means to state quantified statements as well as their propagation across array modifications, do not require any new syntax in the model, only the internal data structures needed extensions to store and process quantified statements.

The following is an already working example of assumption about array using the universally quantified statement, followed by modification of some element in the middle and assignment of the whole to another array:

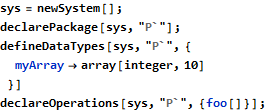
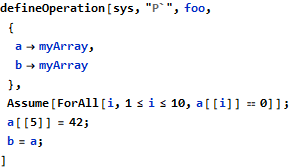
There is a bit of cheating in the above model, as the assumption is made about a local array a. None of the target programming languages can support it without additional tweaking, as local arrays are by default uninitialized, but this simplified example is still sufficient to demonstrate the underlying mechanics of how quantified statements integrate with the existing structures.

The proof statements reveal how the above translates into the evolving set of knowns in each step:

In the above list each index (except start and finish) corresponds to a single line in the body of operation foo and it can be seen that:

• At index 1, the quantified statement was accepted into the list of knowns. It says that all elements of array a, from 1 to 10, are equal to zero.
• At index 2, array a is modified and a new value is assigned to its 5th element. As usual in such modifications, a new version of the array is created and named a1 (with 1 as a subscript). The 5th element has a known value and that was recorded as well. But the most important part of this development is that a new quantified statement was generated for a1, stating that all elements from 1 to 10, except 5th, are equal to zero.
• At index 3, array a is copied to b, which creates a new version of b, named b1. All knowledge about a1 was recreated for b1 after this assignment, including both the 5th element value and the quantified statement about all remaining elements.

The proper handling of such knowledge is essential for further processing of both arrays.

Further articles will demonstrate the remaining building blocks, which are deduction, induction and verification.