About Us Products Articles News Contact Support

Supporting Loop Invariants

This article belongs to the series documenting the reasoning behind and development of new features in the Formal Methods Toolkit.

The previous article presented correct generation of proof statements within While loops, with the following motivating example:

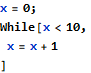
This example code was borrowed from the Wikipedia article about loop invariants, which also provides formal background on the concept. Invariants are design tools that allow to relate the work performed within the loop with the knowledge from before and after the loop, which was the missing part in order to demonstrate, statically, that after the above loop executes, x has value 10.

The formal logic governing the reasoning about loop invariants is described as:

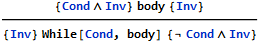
where Cond is a loop condition and Inv is an invariant - a well-intended statement that is supposed to hold before, within and after the loop.

The interesting part of this logic is that it is an inference rule - that is, it says nothing about the case where the rule condition is not met, for example when the invariant is not retained by the loop body or when it was never True in the first place. These cases are not interesting from the engineering perspective and the whole can be simplified by turning the inference rule into assertion. In other words, if the engineer introduces the loop invariant into the design, it can be treated as an obligation. This increased rigour makes the reasoning simpler.

In order to implement this idea in FMT the following syntax was introduced:

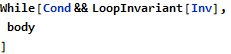
The parser recognizes the new element LoopInvariant and if it is present, the whole loop is transformed into something like this:

Such a structure is simpler than an inference rule with its conditional nature and more rigorously expresses the engineering idea that loop invariant is part of the design contract.

With this support in place the code from the previous article, repeated below with added loop invariant, can be fully verified:

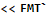
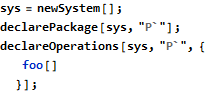
The important additions in relation to the table shown previously are:

• 4 - it is known that x2 <= 10, based on the loop invariant.
• 6 - the implicitly introduced assertion (x3 <= 10) holds, too, which ensures that the invariant is retained across the loop body.
• 7 - the context from the branch (from within the loop) is joined with the enclosing context and the new version of x, which is now x4, is created; this new version is determined to have value 10, based on the invariant resolution at the end of the loop.
• 8 - finally, the user assertion is trivially met, which was not possible before.

All conditions are now satisfied (and reduced to nothing, hence the resulting list is empty):

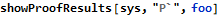
Loop invariants will be officially supported from FMT 2.0.