

|
 |
||
|
This article belongs to the series documenting the reasoning behind and development of new features in the Formal Methods Toolkit.
Previous articles presented the development of features related to quantified statements and loop invariants. These features are only seemingly unrelated - in fact, using them together allows to uncover their greater verification potential.
The following example focuses on a very simple operation that is supposed to fill a given array with zeros. With some necessary supporting definitions, this requirement is stated in the operation post-condition:

The operation declaration involves a post-condition that makes the following promise: after the operation is complete, the given array is entirely (using the convention of indexing from 0) filled with zeros.
The following operation definition combines the use of loop invariants with implicit and explicit operations on quantified statements to achieve the goal stated in post-condition:

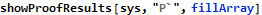

The tool was able to automatically verify that the post-condition is true based on the code above (in fact, many other verification conditions were satisfied as well) and there is nothing to report. Still, there is a lot of happening behind the scenes and since this example demonstrates a foundation for the whole verification approach, it makes sense to deconstruct it step by step.
General idea.
A general idea in the verification of this program is to identify the following invariant: while progressing through the array from lower to higher index values, the part that was visited so far (that is, with indices smaller than the current one) is already filled with zeros. Formally, the loop invariant is:

By convention this invariant happens to be trivially true also at the very beginning, even before updating any of the array elements, when the region described by the quantifier condition is an empty set.
Step 1.
The index variable is initialized to 0. This variable is used to iterate over the array.
Step 2.
This is where the While loop starts operating, as far as the program author is concerned. But implicitly (see the article about loop invariants) there is an Assert injected just before the loop, verifying that the loop invariant is true - and it is, because at that point index is 0 and the applicable region:
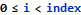
is empty.
Step 3.
At this step the loop actually kicks in. The Synthesize[arraySize] resolves to the value 5 and is needed, because arraySize alone would not be recognized by the grammar. The loop is unrolled once to identify those objects that are modified and their link with the history from before the loop is intentionally broken (see here why). That is, the only knowledge about those objects is that maintained by loop condition and loop invariants. The loop condition states that index < 5 and that’s the only thing that is known about this variable within the loop, in addition to its type constraints. This knowledge is not sufficient to verify the correctness of array accesses, so an additional loop invariant index >= 0 was added to take care of that (going back to Step 2., that additional invariant is checked by means of Assert, as well, and it passes as index was already initialized at that point).
Step 4.
At the beginning of the loop body, before the code that was explicitly written by the loop author, the implicit Assume instructions are injected to establish both loop invariants. This is the knowledge that the rest of the loop has to rely on and maintain.
Step 5.
The array element is updated:
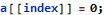
This is accompanied by checks that index is within the range, but the loop condition and additional loop invariant both give enough knowledge to satisfy this check. At that point, the existing quantified statement is retained, because the updated element happens to be just outside of the range established by the loop invariant. That, is, the quantified statement known so far was:

and since the array is updated in a way that does not disturb this quantified statement, it is retained.
Step 6.
The Induce statement checks whether it is possible to extend the existing quantified statement by one step, by checking it if holds also at the following point:

The knowledge gained (or retained) in Step 5. above is sufficient to approve this expansion, which allows to create the following quantified statement, valid in a wider range (note: less than or equal):

This expanding of quantified statement that was also chosen to be a loop invariant is the major point of this approach, as it allows the loop invariant to “follow” the loop execution.
Step 7.
The index value, which plays the role of loop counter, is increased:
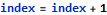
After this operation the quantified statement is again “just behind” the loop counter - its range stays unmodified, but the index value makes a step forward, so (note: less than again):

Step 8.
At the end of loop body, there is an implicit Assert that checks whether the loop invariant (actually, both of them) is still valid. The quantified statement is still correct (both its range and index made a step forward) and also index is still non-negative.
Step 9.
Just after the loop there is an Assume statement that retains the knowledge that was maintained as a loop invariant. That is, this step exports the knowledge maintained within the loop to the context outside of it. This knowledge consists of the quantified statement, the additional constraint that index is non-negative (this fact is not useful any longer) and a negated loop condition. That is, at this step the following are known:

Step 10.
At the very end of the operation the post-condition is verified. The check passes based on the knowledge accumulated so far.
It should be noted that from the FMT point of view there are a few more steps in this whole sequence and all of them are reported by function showProofStatements. The additional steps result from invariants being asserted and assumed one-by-one and from establishing links between different versions of modified variables. Still, the above list is conceptually complete in the sense that it gives the user sufficient framework for designing this and similar programs.
The list of knowns reported at the end of this operation is :
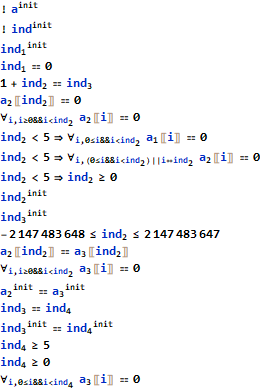
It should be also noted that Step 6. can be potentially automated. This automation can take place at the point of array modification, where decision is taken whether existing quantified statements can be retained for the new array version and where the old statements could be also checked for expansion at the updated position. The possible improvement in this area will be explored in one of the future articles.