

|
 |
||
|
This article is the first in a series that is intended to demonstrate the flexibility of Mathematica as a foundation platform for Formal Methods. The evolution of the Formal Methods Toolkit (FMT) is a major motivation for this series.
The following logic expression has a possible problem:
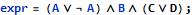
The problem is that the first part of this expression is invariant (it always has the same value True irrespective of the actual value of variable A), which most likely was not intentional and can be a result of programming mistake. Indeed, the expression is easily simplified:
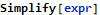
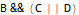
Such a construct can be also a problem with MC/DC testing, where it is required to demonstrate that individual conditions independently affect the result. In this case, variable A has no effect on the complete expression and so it is not even possible to create an appropriate set of such tests.
There is an added value from having static checks verifying that each logic subexpression has reachable both True and False values. Implementing such checks is relatively easy in FMT.
As a first step, the list of all distinct subexpressions, including stand-alone symbols, can be extracted with the standard Cases function:
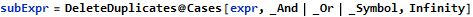
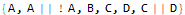
The above assumes that only And and Or operations are relevant, which is the case in FMT (negations are not interesting here). Once such a list is ready, the checks can be easily generated by asserting that it should be both possible for any given subexpression to have True and False values:
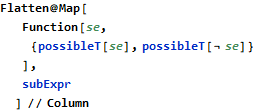

That’s all! The possibleT tag is an FMT’s internal representation of the assertion that the given statement is possible - it is checked by verifying that there exists at least one solution with the used variables at the given point in the program (it is different from the more usual alwaysT tag, which verifies that there is no solution for the negated statement). The fourth statement from the resulting list above is expected to fail, because the following has no solution:

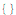
The actual implementation requires some minor polishing, for example to ensure that human-readable descriptions are generated together with these statements.
Below is an example FMT session with a program that uses the same expression in the If statement:
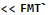


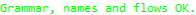
Finally, filtered list of proof results can be displayed to show the ineffective subexpression:
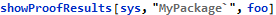

This feature will be available in FMT 2.0.