

|
 |
||
|
This article belongs to the series documenting the reasoning behind and development of new features in the Formal Methods Toolkit.
Ghost variables can be very helpful in system verification, as they allow to reason about the program correctness by referring to values that are fully handled by static means, with no need to exist at run-time.
As a motivating example, two operations can be bound by the requirement that one has to be called before another one is executed - like engines need to be started before the rocket can be launched, or user input must be validated before it is processed, and so on. It is possible to model such requirements with the use of a dedicated variable (in such cases a single Boolean variable would be sufficient) - for example, the user input validation operation could set that variable to True to indicate that the validation step was done and then the input processing operation could check the same variable to determine whether the data was already validated. In some cases it appears, however, that once such a check is statically verified, the reason for the variable to exist at run-time disappears and it can be handled entirely in the static domain. Such variables are called ghosts.
Introducing some basic support for ghost variables is relatively straightforward in FMT, where the verification is performed by solving symbolic equations where symbols are generated to reflect actual variables used in the model, including all supporting statements from pre- and post-conditions. From this perspective, a ghost variable is just another symbol that can be used in verification statements without any special treatment, except for the need to inform the solver about the intended domain of the variable. Since the solver at the lower level operates on Integers and Booleans domains only (user-defined types are ultimately mapped to them, with range constraints and type invariants added to the set of expressions), these are the most natural choices for ghosts as well.
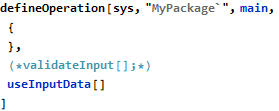
A new function in FMT is needed so that domains for ghost variables can be provided to the solver, with the intended use as in:
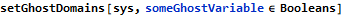
The above states that someGhostVariable belongs to the Booleans domain and this is remembered within the model sys, so that further uses of that variable do not need to be obscured with the same information anymore - this is conceptually similar to declaring a regular variable in the model. For convenience, this function will accept both single or multiple (listed) domain associations.
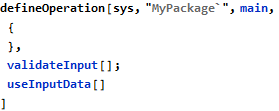
With this simple support the following will be possible:

There are three operations in this model, with validateInput and useInputData being related in the way that validateInput promises to set the inputValidated variable and useInputData expects that variable to be already True when it is invoked.
The main operation can be defined to test this relation:
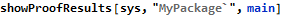
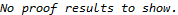
There are no proof results to show, because all tautologies and trivial statements are simplified and removed, so at the end there is nothing interesting to solve - which indirectly shows that there are no errors in this program. As a sanity-check, it is still possible to see the generated verification statements:
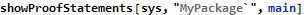

The above output means that from two steps within the main operation, the first (which is a call to validateInput) establishes that inputValidated is True, which is exactly what the second step (which is a call to useInputData) expects as its pre-condition.
When the first step (the call to validateInput) is omitted or commented out, the results are different:

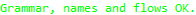
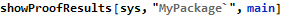

with counter-examples displayed in the tool-tip as:

In other words, the requirement to always have the input validated before it is used was verified with the use of some artificial variable that does not need to exist in the model as a run-time value.
The interesting part of this example is that the relation between two operations was verified without even implementing these operations, based only on their pre- and post-conditions. What was silently skipped so far was that at some point the validateInput operation will need to be implemented, too, and its post-condition will be verified against its body, where the ghost variable cannot be just set as any other variable declared in the model. That is, it is not possible to write:
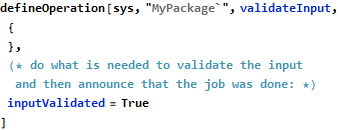
because inputValidated is not recognized by grammar checks as a legal variable. Still, after a minor modification in grammar rules for verification statements, it will be possible to use ghost variables in the Assume construct, which collects the verification “knowns”, like here:
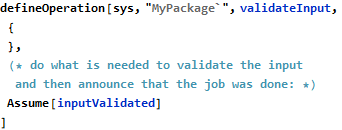
As far as the solver is concerned, the above is equivalent to setting inputValidated to True. This approach might look slippery as the Assume construct has the ability to inject arbitrary knowledge, including the wrong one, and is therefore considered dangerous - but in this context it is not any more dangerous than imperative assignment to some arbitrary state variable and it might actually be more appropriate as it better attracts attention during reviews.
Another simple example shows that it is also possible to use “ghost functions” - that is, functions that are not part of the model (and consequently are not part of the generated source code) and that refer to ghost variables to build some more complex expressions. In this model it is expected that at least one of the two engines are running before the rocket is launched, with the ghost function named someEnginesRunning defined to give the green light for the launch:

Again, removing the call to rightEngineStart from main causes the verification to fail. The ghost symbols leftEngineRunning, rightEngineRunning and someEnginesRunning never make it to the generated source code, because even though they are used to reason about the model, they are not part of it.
This basic support for ghost variables has a natural limitation that only simple Integers and Booleans values are allowed - that is, no ghost arrays or structures are possible. This limitation comes from the fact that ghost variables are decoupled from the model and are not handled by the main grammar and expression processing engine. On the other hand (and for the same reason), they are not constrained by the FMT grammar and therefore can be manipulated in ways that are potentially much more expressive and powerful.
The setGhostDomains function and the relaxed grammar rules for Assert and Assume will be available in FMT 2.0.